
........Dispositivos para el control acústico
[10][11][12]
Uno de los problemas más importantes a resolver en las salas de música consiste en la creación de un campo sonoro muy difuso, esto es, que el sonido sea envolvente. Para esto es necesario evitar, en lo posible, las reflexiones especulares en algunos lugares.
En los teatros antiguos la difusión se logra mediante balcones, estatuas, adornos, etc. pero esto resultaría muy costoso y poco estético para los patrones actuales. Por ello se han diseñado dispositivos de dispersión controlada los cuales se basan en paneles de ciertas geometrías.
A partir de una extensa evaluación subjetiva de salas de conciertos Europeas, se [10] encontró que la diferencia biaural de las señales que llegan a los oídos estaba altamente correlacionada con los datos de preferencia subjetiva.
La similaridad Biaural ( o Coherencia interaural) se define como el valor pico de la función de correlación de los primeros 80 ms de la respuesta impulsiva dentro de una diferencia de retardo interaural de 1 ms. La diferencia biaural es el negativo de la similaridad Biaural.
Todo esto implica que el sonido que llega en el plano medio del oyente es perjudicial para la preferencia subjetiva ya que, al recibir por igual las ondas de presión sonora en ambos oídos, se produce un efecto "Monofónico" en lugar del agradable " Estéreo ".
Estos resultados también se correlacionaron fuertemente con aspectos físicos de la sala: mientras más altas eran, mayor era la preferencia, ya que el oyente recibía una mayor cantidad de reflexiones laterales tempranas.
En la actualidad no resulta conveniente la construcción de salas con techos altos y paredes laterales cercanas por múltiples razones:
Para aumentar la diferencia biaural en las salas modernas podría pensarse en la absorción de las señales que inciden en el techo pero esto, en salas de 1000 o más asientos constituiría un enorme despilfarro de energía acústica. La solución ingenieril correcta es la de redireccionar la energía sonora de manera que llegue directa o indirectamente en forma lateral al escucha.
A partir de estos requerimientos el Profesor M. R. Schroeder [10] desarrolló una estructura cuya superficie produce una excelente difusión del sonido en un gran intervalo de frecuencias.
El objetivo básico planteado es el de obtener una superficie capaz de reflejar una onda incidente en todas direcciones, para lo cual supongamos que tenemos una estructura como la indicada en la figura V.21. Como se puede observar consiste en una serie de rendijas.

Cada rendija se comporta como una fuente sonora pero con un retardo igual al doble de su profundidad, luego el problema se limita a encontrar cual debe ser la secuencia de profundidades para que el patrón de difracción de la estructura sea lo más uniforme posible.
En general tenemos:
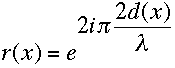 (V31)
(V31)
donde:
r(x) = factor de reflexión.
d(x) = profundidad de la rendija en la posición x.
Utilizando la teoría de Fraunhofer de campo lejano tenemos que la amplitud de la dispersión a(s) es igual a:
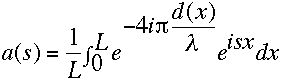 (V32)
(V32)
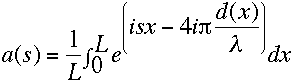 (V33)
(V33)
donde la magnitud del vector de dispersión s está relacionada con el ángulo incidente y el de difracción por:
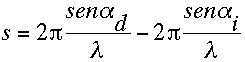 (V34)
(V34)
si aproximamos la integral de la ecuación V.31 con una sumatoria tenemos:
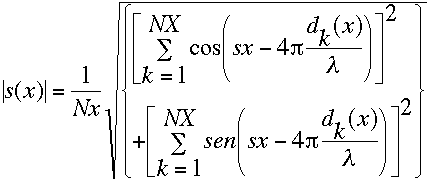 (V35)
(V35)donde:
dk(x)=Profundidad
NX=Número total de muestras de profundidad
Una solución interesante se tiene si hacemos que las profundidades sigan una secuencia dada por:
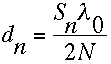 (V.34)
(V.34)
donde Sn = n2 mod(N)
N es un número primo y n entero menor de N
ya que para, esta serie, la función de la ecuación V.33 se aproxima a 1, lo cual era lo deseado. Este tipo de difusor se denomina de Residuos Cuadráticos.
El diseño del difusor se limita al siguiente procedimiento:
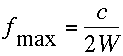 (V.35)
(V.35)donde W es el ancho de cada rendija y c es la velocidad del sonido, en otras palabras w es igual a la media longitud de onda de la frecuencia máxima.
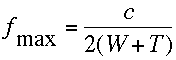 (V.36)
(V.36)
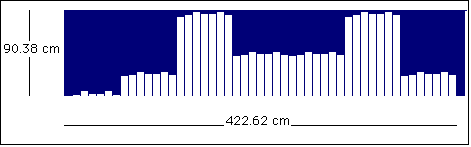
En la figura V.22 se tiene un ejemplo de un difusor con residuos cuadráticos, mientras que su diagrama de difracción se encuentra en la figura V.23.
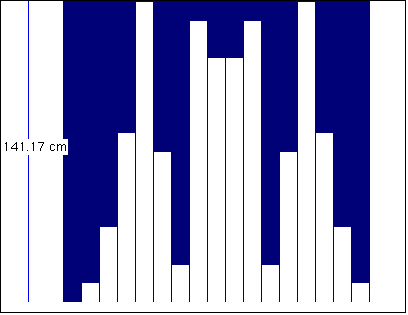
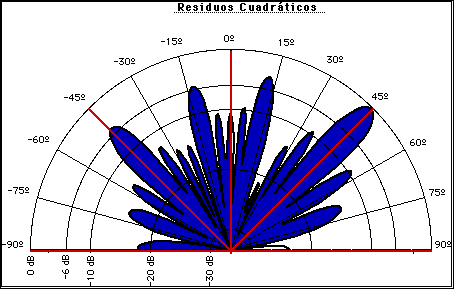
Los difusores de residuos cuadráticos tienen entre sus características la de incluir entre los lóbulos de difracción al reflejo especular.
En algunos casos sería interesante colocar un sistema difusor que no incluyera el reflejo especular, por eso el Prof. Schroeder desarrolló un tipo de secuencia con esa característica: El Difusor basado en raíces primitivas.
La secuencia, en este caso, es:
donde:
N = Número primo
n = entero menor que N
g = raíz primitiva de N.
Para que g sea raíz primitiva de N debe cumplirse que, para n entre 1 y N-1 no debe repetirse ningún resultado de gn mod (N).
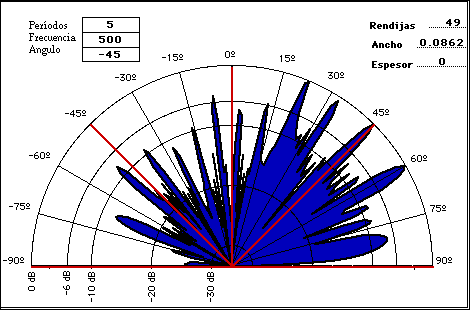
En la figura V.24 se tiene un ejemplo de un difusor con raíces primitivas, en la figura V.25 se demuestra su patrón de difracción el cual tiene atenuado el reflejo especular.
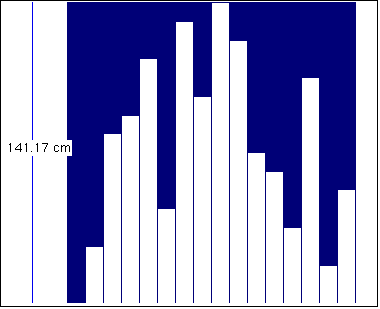
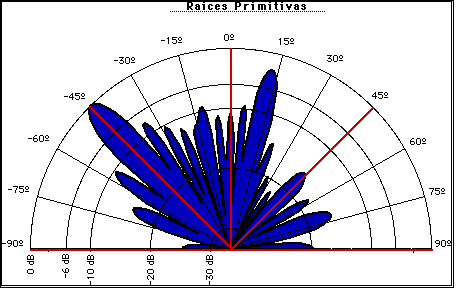
Recientemente P. D'Antonio y J. Konnert [11][12] han desarrollado una versión de un difusor basado en residuos cuadráticos con una dimensión fractal. En este caso la secuencia de profundidades viene dada por:
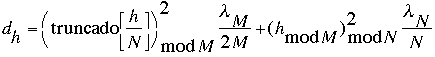 (V.38)
(V.38)donde:
M número primo para la difusión en baja frecuencia.
N número primo para la difusión en alta frecuencia.
h número de la rendija.
lM longitud de onda de diseño para baja frecuencia
lN longitud de onda de diseño para alta frecuencia
dh profundidad de la rendija h
Los difusores estudiados hasta el momento funcionan solo en el plano formado por el ángulo de incidencia de la onda, pero estudios posteriores han determinado secuencias Bidimensionales que permiten distribuir la energía acústica de la onda incidente en todo el espacio.
Así tenemos que el equivalente bidimensional del difusor de residuos cuadráticos viene dado por la secuencia:
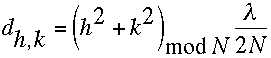 (V.39)
(V.39)donde:
N Número primo.
h,k número de sector. Enteros entre 0 y N-1
dh,k profundidad del sector h,k
Por ejemplo para un número primo igual a 7 la secuencia sería:
|
0 |
1 |
4 |
2 |
2 |
4 |
1 |
|
1 |
2 |
5 |
3 |
3 |
5 |
2 |
|
4 |
5 |
1 |
6 |
6 |
1 |
5 |
|
2 |
3 |
6 |
4 |
4 |
6 |
3 |
|
2 |
3 |
6 |
1 |
1 |
6 |
3 |
|
4 |
5 |
1 |
6 |
6 |
1 |
5 |
|
1 |
2 |
5 |
3 |
3 |
5 |
2 |
luego basta con multiplicar por l/(2N) para tener las profundidades.
Para tener una versión similar a la de raíces primitivas pero bidimensional se utiliza una secuencia basada en el teorema del Resto Chino. esto es:
1.- Se elije un número primo N.
2.- Se calculan los factores co-primos de N ( N1 y N2), esto es, dos números no divisibles entre sí que multiplicados dan N-1.
3.- Se diseña una matriz de 0 a N1-1 columnas y de 0 a N2-1 filas
3.- Se hace variar un número entero h a partir de 0.
4.- Se asigna el valor de profundidad :
(V.40)
a la coordenada dada por:
Columna
h mod N1
fila
h mod N2
Esta secuencia de profundidades garantiza que el reflejo especular estará atenuado.
Por ejemplo si elegimos N=43 sus factores co-primos son 6 y 7 quedando la siguiente matriz:
|
0 |
36 |
30 |
24 |
18 |
12 |
6 |
|
7 |
1 |
37 |
31 |
25 |
19 |
13 |
|
14 |
8 |
2 |
38 |
32 |
26 |
20 |
|
21 |
15 |
9 |
3 |
39 |
33 |
27 |
|
28 |
22 |
16 |
10 |
4 |
40 |
34 |
|
35 |
29 |
23 |
17 |
11 |
5 |
41 |
Por último se tiene una versión bidimensional fractal con residuos cuadráticos
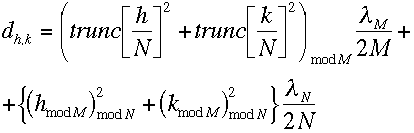 (V.41)
(V.41)donde:
M = número primo para la difusión en baja frecuencia.
N = número primo para la difusión en alta frecuencia.
h,k = coordenada del sector.
lM = longitud de onda de diseño para baja frecuencia
lN = longitud de onda de diseño para alta frecuencia
dh,k = profundidad del sector h,k
Para una frecuencia mínima de 100 Hz y una superior de 2000 , con M=N=3 tenemos las siguientes profundidades:
|
0 |
3 |
3 |
57 |
60 |
60 |
57 |
60 |
60 |
|
3 |
6 |
6 |
60 |
63 |
63 |
60 |
63 |
63 |
|
3 |
6 |
6 |
60 |
63 |
63 |
60 |
63 |
63 |
|
57 |
60 |
60 |
115 |
118 |
118 |
115 |
118 |
118 |
|
60 |
63 |
63 |
118 |
120 |
120 |
118 |
120 |
120 |
|
60 |
63 |
63 |
118 |
120 |
120 |
118 |
120 |
120 |
|
57 |
60 |
60 |
115 |
118 |
118 |
115 |
118 |
118 |
|
60 |
63 |
63 |
118 |
120 |
120 |
118 |
120 |
120 |
|
60 |
63 |
63 |
118 |
120 |
120 |
118 |
120 |
120 |
Dispositivos para control de transmisión de sonido..........